5 октября 2021

Число

Число - одно из основных понятий математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.

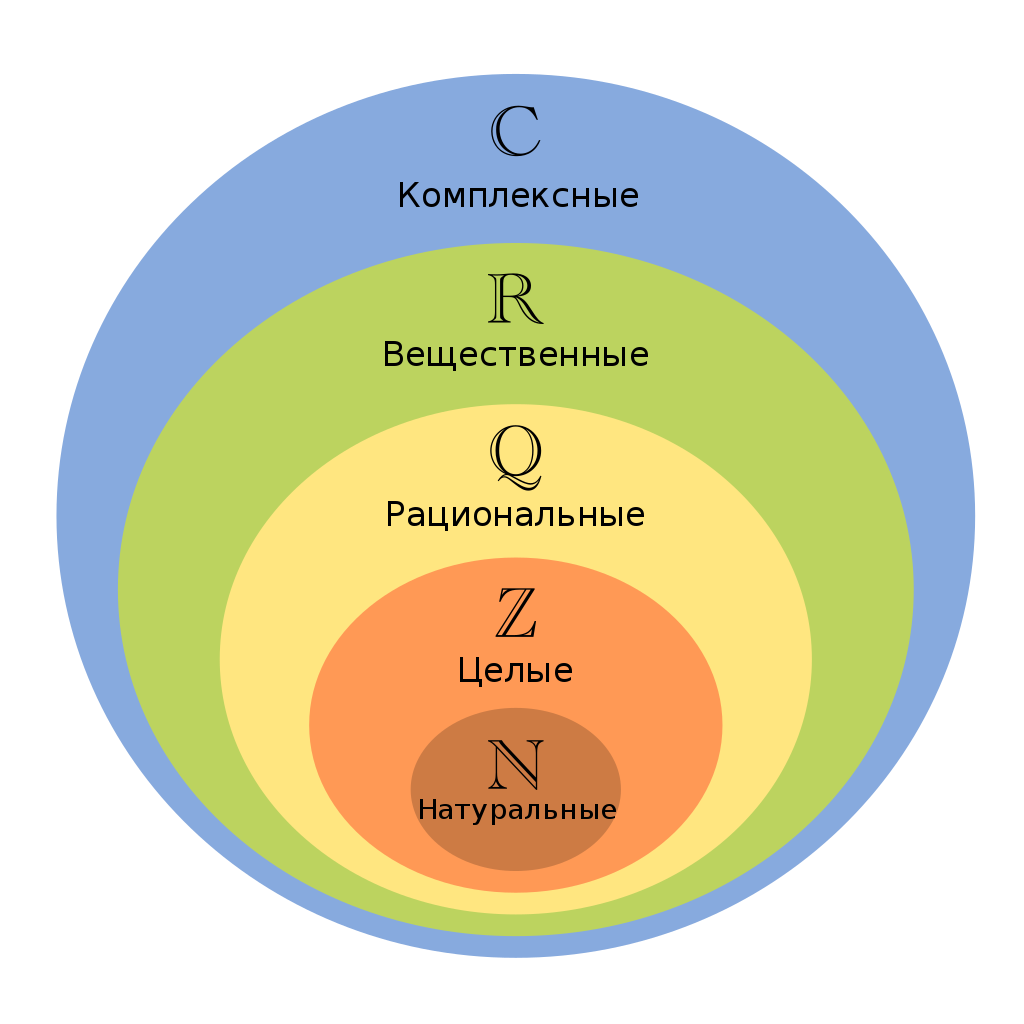
Традиционно выделяют следующие множества чисел, каждое из которых включает все предыдущие:

• Натуральные числа ℕ = {1, 2, 3, …}
• Целые числа ℤ = {…, -2, -1, 0, 1, 2, …}
• Рациональные числа ℚ - числа, представимые в виде дроби, числитель которой является целым числом, а знаменатель - натуральным
• Действительные числа ℝ. Множеству дейситвительных чисел можно поставить в соответствие множество всех точек на прямой. Действительные числа включают рациональные и иррациональные числа. Последние нельзя представить в виде дроби (например, число пи).
• Комплексные числа ℂ. Множеству комплексных числел можно поставить в соответствие множество всех точек на плоскости.

Позиционные системы счисления

Система счисления - символический метод записи чисел, представление чисел с помощью письменных знаков.

Классификация систем счисления:

• Непозиционные
• Позиционные

Пример непозиционной системы счисления - римские цифры:

1	5	10	50	100	500	1000
I	V	X	L	C	D	M

В непозиционных системах значение символа (цифры) не зависит от положения в записи числа.

В позиционных системах счисления значение цифры зависит от ее позиции (разряда).

Цифра - сивол для записи чисел.

Разряд - индекс цифры в обозначении числа.

Основание системы - количество единиц одного разряда, составляющее единицу соседнего, более старшего разряда.

Привычная нам система счиаления - позиционная с основанием 10 (десятичная). В качестве символов мы используем арабские цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Для подсчета секунд, минут и часов мы используем шестидесятиричную систему. Для подсчета количества дней и недель мы используем семиричную систему. Информация в компьютере всегда хранится в двоичной системе.

Перевод чисел из одной системы в другую

Алгоритм перевода записи числа A из десятичной системы счисления в систему с основанием r:

1. Определяем переменную B, присваеваем ей значение A
2. Находим остаток от деления B на r - это очередная искамая цифра
3. Присваиваем переменной B значение от целочисленного деления B на r. Если B не равно нулю, возвращаемся на шаг 2
4. Выписываем полученные цифры в обратном порядке

Пример 1. Переведем число 34 в семиричную систему.

B = 34
34 % 7 = 6  (цифра младшего разряда)
B = B / 7 = 4
4 % 7 = 4   (цифра следущего разряда)
B = B / 7 = 0

Получаем, что число 34 записывается в семиричной системе как 46.

Перевод записи числа A из системы с основанием r в десятичную выполняется следющим образом. Пусть A представлено следующими символами:

a[1] a[2] a[3] ... a[n]

Тогда, выполняя следующие операции в десятичной системе, получим нужный резулдьтат:

A = a[n] + a[n-1] * r + a[n-2] * r^2 + ... + a[1] * r^{n-1}